Solving quadratic equations or finding the roots of equations of second degree is a popular problem in many programming languages. The equations of second degree which resemble the standard form: ax 2+bx+c=0, are known as quadratic equations. A large number of quadratic equations need to be solved in mathematics, physics and engineering. In this tutorial, we’re going to discuss a program for Solving Quadratic Equations in C programming language. Fta Dish Channel List Download Sites. Here, I’ve briefly discussed the working mechanism or algorithm for solving quadratic equations in C; the algorithm can be used to write a program to solve quadratic equations in any high level programming language.

Oct 7, 2014 - Solving quadratic equations or finding the roots of equations of second degree is a popular problem in many programming languages. The equations of second degree which resemble the standard form: ax2+bx+c=0, are known as quadratic equations. A large number of quadratic equations need to be. This C Program calculates the roots of a quadratic equation. First it finds discriminant using the formula: disc = b * b – 4 * a * c. There are 3 types of roots.

The program source code, as shown in the output screens, is applicable for both types of roots of the quadratic equations: real and imaginary. Algorithm: The working principle of this program to find the roots of a quadratic equation is similar to manual algebraic solution. The calculation procedure or the formulas to find out the roots is same. The program presented here follows the following steps: • Enter the value of a, b and c • After getting these values, the program calculates the value of discriminant, dis= b 2-4ac. • It checks the value of discriminant whether it is less than zero or greater than zero.

• If the dis. } This program to find the roots of quadratic equations has two header files: stdio.h and math.h. The first header file is to control the console inputs and outputs whereas the math.h is for finding out the square roots during calculation of discriminant.

As the program is executed, it asks for the values of a, b and c which have been defined as float data type; it is better to use float than int as the roots mostly come in decimal points. Top2048 Programmer Software. Then, the program calculates the value of discriminant and compares it with 0.

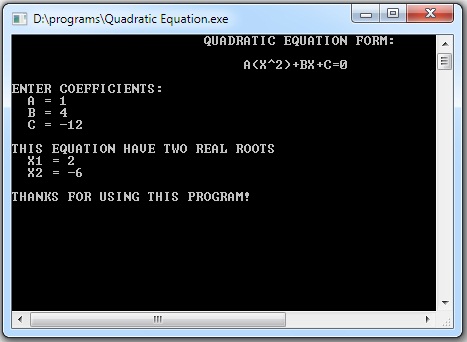
If the discriminant is found to be less than zero, the values of imaginary roots are displayed, otherwise the real roots are displayed as solution. When the values of a, b and c are entered as 1, -5 and 5, real roots are displayed.

For input values of 4, 5 and 6, the roots come out to be imaginary as shown in the output screens below. Abbyy Screenshot Reader Portable Full more. Real Roots Imaginary Roots This source code for solving quadratic equations in C is short and simple to understand. You need to compile the source code in Code::Blocks IDE. If you have any queries or suggestions regarding this post or source code, mention/discuss them below in the comments section.

You can find more C Tutorials here.

Ok, so I am in my first c++ college course. I have done programming before in java, html, sql and some basic c++ stuff before.

I find the class to be easy so far but I am actually stuck on this homework assignment. The assignment is as follows: Write a C++ program that solves quadratic equation to find its roots.

The roots of a quadratic equation ax2+bx+c=0 (where a is not zero) is given by the formula: x=(-b±√(b^2-4ac))/2a Note:To find the square root of a number, use the function sqrt() and include the math library. Where (b^2-4ac) is the discriminant. If the value of the discriminant is zero then the equation has a single real root. If the value of the discriminant is positive then the equation has two real roots. If the value of the discriminant is negative, then the equation has two complex roots.

Here is the sample output that they gave me to outline my code. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 example 1: Enter the values for a, b and c 1 3 -4 The discriminant is 25 The equation has two real roots. The roots of the quadratic equation are x=-4,1 example 2: Enter the values for a, b and c 2 -4 -3 The discriminant is 40 The equation has two real roots.